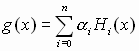
Autor
Marcin Wudarczyk, K2, MiNI
Zadanie
Aproksymacja średniokwadratowa na przestrzeń wielomianów z bazą wielomianów ortogonalnych Hermite'a z wagą exp(-x*x) na przedziale (-Ą ,+Ą ). Całkowanie metodą 5-cio punktową Gaussa-Hermite'a.
Metoda
Funkcja interpolacyjna jest postaci 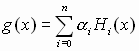
Znalezienie funkcji interpolacyjnej polega na znalezieniu liczb a i z równania macierzowego
![]() ; gdzie G - macierz Gramma: G(k, l) = (Hk, Hl);
; gdzie G - macierz Gramma: G(k, l) = (Hk, Hl); ![]() , i 0 dla różnych indeksów.
, i 0 dla różnych indeksów. ![]() ,
, ![]() .
.
Norma ![]() . Ponieważ większość elementów macierzy Gramma jest zerowa, rozwiązanie układu jest trywialne.
. Ponieważ większość elementów macierzy Gramma jest zerowa, rozwiązanie układu jest trywialne.
Całkę wylicza się jako sumę wartości funkcji w miejscach zerowych 4-go wielomianu Hermite'a z odpowiednimi wagami.
Implementacja
Program wykonano w C++Builder 5.0 pod Windows. Użyto zmiennych podwójnej precyzji, oraz stablicowanych miejsc zerowych i wag z dokładnością do 6 miejsca po przecinku.
Program
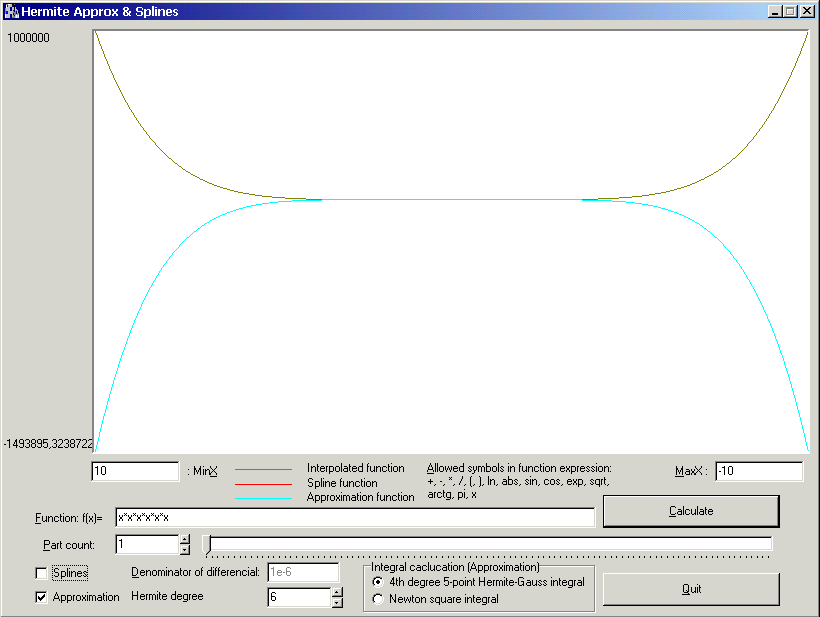
W głównej części okna programu znajduje się wykres, zgodnie z opisem pod nim wyświetlane są wykresy funkcji interpolowanej, funckję uzyskaną w wyniku aproksymacji, oraz, ewentualnie, funkcję powstałą przez interpolację Spline. Poniżej można wybrać funkcję, przedział interpolacji i ilość podprzedziałów - dotyczy spline'ów i całkowania złożoną formułą prostokątów, oraz wyświetlone wykresy i wymiar przestrzeni wielomianów interpolacyjnych.
Zadania przykładowe
Zadanie 1
f(x) = x4-4x2
Wynik:
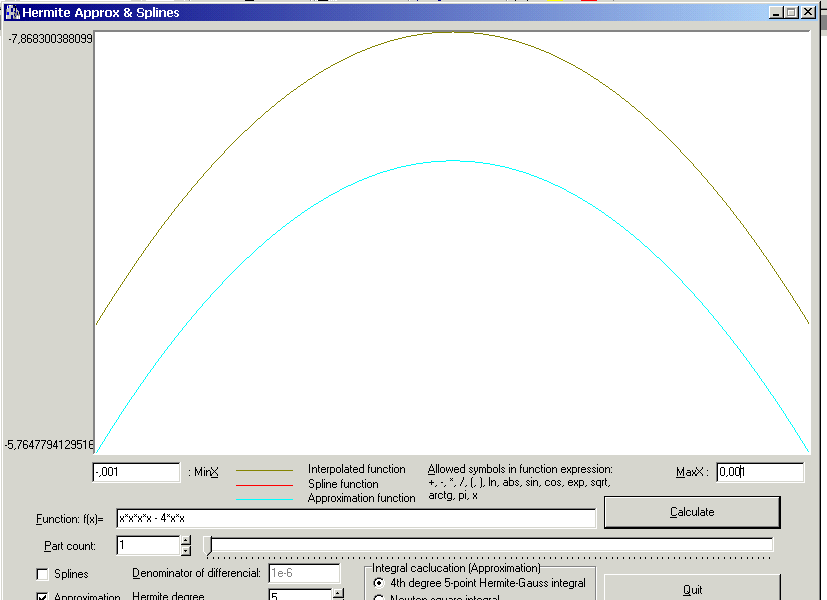
Zadanie 2
f(x)= x4-4x2
Wynik: 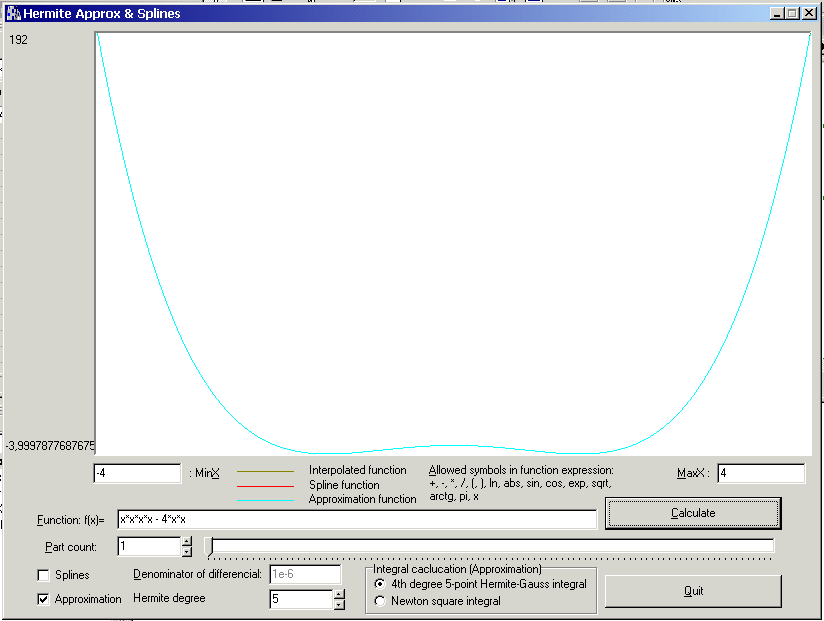
Zadanie 3
f(x)=x5
Wynik: 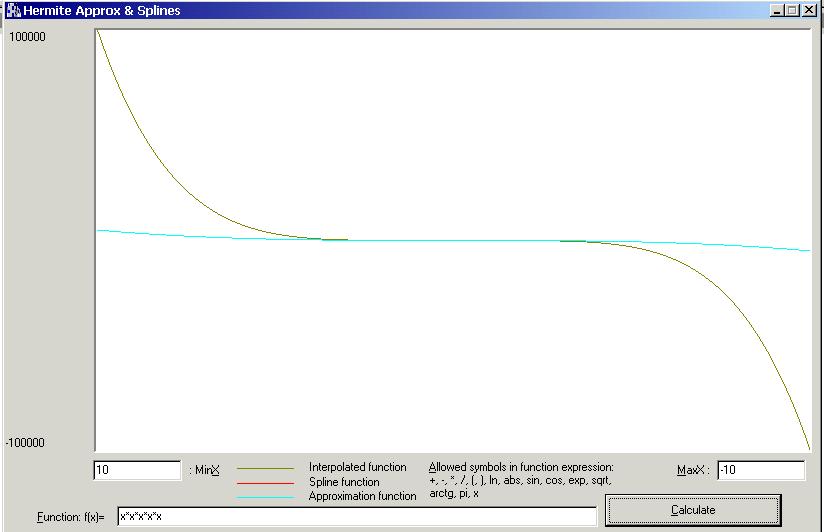
Zadanie 4
f(x) =x6
Wynik: