Autor

Marcin Wudarczyk, K2, MiNI

Zadanie

Napisać program znajdujący miejsce zerowe wielomianu w dziedzinie zespolonej metodą siecznych.

Metoda

Metoda siecznych, wskazania w zadaniu, jest metodą iteracyjną. Wymaga dwóch punktów początkowych.

Oznaczenia:

w wielomian stopnia n

x* dokładne miejsce zerowe: w(x*) = 0

x^(k) k-te przybliżenie miejsca zerowego

x⁽⁰⁾, x⁽¹⁾ przybliżenia początkowe

M₂ maximum z wartości drugiej pochodnej w dziedzinie

m₁ minimum z wartości pierwszej pochodnej w dziedzinie

e żądana dokładność

|| || norma dla liczb zespolonych:

Ogólnie dla metod iteracyjnych:
,
gdzie A i p zależą od metody. W przypadku metody siecznych A = M₂/2/m₁ a p @ 1,6.

Kolejne przybliżenia znajdujemy wzorem: .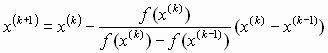

Nie jest gwarantowane, że dla wszystkich danych metoda jest zbieżna, ani, że kolejne przybliżenia nie wyjdą poza dziedzinę.

Zatrzymanie iteracji następuje, gdy.

W praktyce stosuje się prostsze warunki.

Implementacja

Program napisano w języku C++. Użyto kompilatora Borland C++Builder 4.0. Program działa pod systemami operacyjnymi Windows 95 lub Windows NT lub późniejszymi.

Obliczenia są przeprowadzane na typie podwójnej precyzji. Użyto standardowej bilbioteki liczb zespolonych języka C++.

Sednem programu jest funkcja solve, która jest implementacją metody siecznych. Jako argumenty przyjmuje wielomian, przybliżenie i żądaną dokładność. Zwraca prawdę, gdy zostało znalezione miejsce zerowe po mniej niż 100.000 iteracjach.

Jako warunek stopu przyjęto .

Program

Po uruchomieniu programu wypisane zostaną aktualne ustawienia programu, tj. wielomian, punkty początkowe i dokładność obliczeń. Poniżej pojawi się lista dostępnych poleceń. Wybór polecenia następuje poprzez wciśnięcie klawisza odpowiadającego cyfrze wyświetlonej obok polecenia. Są to:

Wprowadzanie wielomianu: po wybraniu tej opcji program zapyta najpierw o stopień wielomianu. Następnie wyświetli kolejne wyrazy wielomianu w formie x^n*[a_n], wraz ze znakiem zachęty do wpisywania współczynników a_n. Współczynniki rzeczywiste wprowadzamy po prostu z klawiatury jako liczby, opcjonalne jest zamykanie w nawiasach współczynników ujemnych. Współczynniki zespolone wprowadzamy w postaci pary (re, im), gdzie re i im to odpowiednio rzeczywista i urojona część liczby zespolonej.

Ustawienie punktów początkowych: program poprosi o podanie liczb x₀ i x₁. Format liczb taki sam jak w poprzednim poleceniu.

Ustawienie dokładności: ustawia dokładność e . Tylko liczby rzeczywiste.

Wykonanie obliczeń: program spróbuje znaleźć przybliżone miejsce zerowe zadanego wielomianu. Gdy je znajdzie, wypisuje je na ekran wraz z wartością wielomianu dla przybliżonej wartości miejsca zerowego. W przypadku nie powodzenia program wypisze stosowny komunikat.

Wyjście z programu: kończy pracę z programem; podobnie działa klawisz ESC.

Zadania przykładowe

Zadanie 1

Wielomian: w(x) = x² + 2

Punkty początkowe: x₀ = 0, x₁ = 1

Dokładność: e = 10^-9

Wynik: program nie może znaleźć miejsca zerowego, ponieważ punkty początkowe nie zawierają części urojonej.

Zadanie 2

Wielomian: w(x) = (2,-1)*x³ + (16,8)*x² + (24,4)*x¹ + (4,0.5)

Punkty początkowe: x₀ = 0, x₁ = (1, 1)

Dokładność: e = 10^-9

Wynik: (-0.190302,-0.00195116)

Zadanie 3

Wielomian: w(x) = (2,-1)*x³ + (16,8)*x² + (24,4)*x¹ + (4,0.5) - ten sam co poprzednio

Punkty początkowe: x₀ = -20, x₁ = (-20, -20)

Dokładność: e = 10^-9

Wynik: (-3.56434,-6.99942)

Zadanie 4

Wielomian: w(x) = (1,-1)*x¹⁰ + (2,-2)*x⁹ + (3,-3)*x₈ + (4,-4)*x⁷ + (5,-5)*x⁶ + (-6,6)*x⁵ + (-7,7)*x⁴ +
+ (-8,8)*x³ + (-9,9)*x² + (-10,10)*x¹ + (3.14,-3.14)

Punkty początkowe: x₀ = 0, x₁ = (1,1)

Dokładność: e = 10^-12

Wynik: (0.24518,-1.67681e-18) » (0.24518,0)