Zadanie *

Definicje *

Algorytmy *

Struktury danych *

Implementacja *

Rysunki *

Mamy siatkę prostokątną o zadanym rozmiarze (większy bok ma n kwadratów jednostkowych - dalej zwanych pixelami). Każdy pixel może mieć jeden z następujących stanów: pusty, wypełniony, jest na nim przynajmniej jeden obiekt. Należy wygenerować w sposób losowy labirynt - tj. ustawić stany każdego pixela na pusty lub wypełniony. Następnie losowo rozmieścić na mapie zadaną ilość tzw. checkpointów, które są obiektami. Każdy checkpoint ma swój numer, numer mieści się w zakresie od 0 do k-1, gdzie k to liczba checkpointów. Następnie do mapy wstawiamy robota (też jest obiektem). Zadaniem robota jest przejście przez wszystkie checkpointy w zadanej kolejności (rosnących numerów checkpointów), nie znanej robotowi. Robot może zapamiętywać dowolne informacje o mapie, ale tylko o pixelach, na które wszedł, ma te informacje.

Operatory mają takie same znaczenie, jak w języku C++. W szczególności, operator == oznacza równość, [] odwołanie do indeksu tablicy. Inne użyte pojęcia są zwykle definiowane w miejscu użycia, lub też są ogólnie znane i przyjęte, np. stos, wektor, kolejka FIFO. W razie niejasności należy się odwołać do książki "Algorytmy i struktury danych", której jednym z autorów jest prof. Diks. Ściana jest to pixel oznaczony jako zapełniony, czyli taki, na który obiekt nie może wejść. Pixel jest to twór, na którym może stać obiekt. Mapa składa się z pixeli.

Przykładowy kod oraz definicje klas zostały napisane w języku C++.

Ogólny schemat postępowania programu:

1. Wygenerowanie mapy, rozmieszczenie checkpointów i robota
2. Znalezienie przez robota wszystkich checkpointów poprzez przeszukiwanie mapy. Jeżeli nie znaleziono odpowiedniej liczby checkpointów, kończymy postępowanie.
3. Znalezienie najkrótszych ścieżek łączących każdą parę checkpointów.
4. Aproksymacyjne rozwiązanie problemu komiwojażera dla grafu checkpointów
5. Przechodzenie po znalezionej ścieżce przez wszystkie checkpointy, aż któryś zostanie zabezpieczony.
6. Sprowadzenie rozwiązania problemu komiwojażera dla poprzedniego grafu checkpointów do rozwiązania dla tego samego grafu, z którego zabezpieczony w poprzednim punkcie wierzchołek został usunięty.
7. Konturujemy postępowanie od punktu 5, aż wszystkie checkpointy zostaną zabezpieczone.

1. Generowanie mapy

Operacja ta będzie przebiegała w następujący sposób:

1. Otoczenie zadanego obszaru prostokątnego przez ściany
2. Wstawienie do mapy łamanych, które mają co najwyżej jeden pixel sąsiadujący z inną ścianą; łamane mają losowy kształt i długość
3. Wstawienie do środka mapy pewnej liczby pojedynczych pixeli-ścian o losowej pozycji.
4. Wstawienie losowo checkpointów

Łamana składa się z uporządkowanych krawędzi. Krawędzie są odcinkami prostymi złożonymi z pixeli z stanem ściana. Każda następna krawędź położona jest w stosunku do poprzedniej pod kątem P /2. Każda następna krawędź ma dokładnie jeden punkt wspólny z każda inną krawędzią, położony na jej początku lub końcu i będący jednocześnie ostatnim lub pierwszym punktem poprzedniej krawędzi.

Parametrami będą:

• Orientacja łamanej - prawoskrętna lub lewoskrętna
• Prawdopodobieństwo tego, że kierunek aktualnie generowanej krawędzi nie zmieni się. W przypadku porażki w próbie z tym prawdopodobieństwem zaczyna się nowa krawędź. Przeciętną długość krawędzi można wyliczyć ze wzoru: długość = 1/(1-p)
• Prawdopodobieństwo tego, że kierunek nowej krawędzi (po zmianie kierunku) nie zmieni się zgodnie z orientacją łamanej. Jeżeli parametr ten jest równy 0.5, to łamana, będzie zrównoważona, w przeciwnym wypadku będzie miała tendencję do "zakręcania" w jedną stronę.

W tej części dokumentu będziemy mówić, że pixel sąsiaduje ze ścianą wtedy i tylko wtedy, gdy przynajmniej jeden z ośmiu pixeli przylegających do niego ścianami lub wierzchołkami jest ścianą (izolowana pixel-ściana nie sąsiaduje ze ścianą).

Łamana sąsiaduje ze ścianą, gdy jeden z pixeli do niej należących sąsiaduje ze ścianą nie należącą do aktualnie generowanej łamanej.

W trakcie postępowania pamiętamy w zmiennej (znacznik), czy generowana łamana sąsiaduje ze ścianą.

Oto algorytm generowania krawędzi:

1. Wylosowanie punktu początkowego. Punkt początkowy nie może być ścianą, ale może sąsiadować ze ścianą - inicjalizujemy odpowiednio znacznik.
2. Zaznaczamy pierwszy pixel krawędzi jako ścianę i losujemy kierunek pierwszej krawędzi
3. Losujemy z odpowiednim prawdopodobieństwem, czy krawędź się kończy. Jeżeli tak, losujemy z podanym prawdopodobieństwem, czy nowy kierunek będzie zgodny z orientacją, czy nie..
4. Rozpatrujemy następny pixel wzdłuż nowego kierunku. Sprawdzamy, czy nie sąsiaduje ze ścianą. Jeżeli sąsiaduje, to sprawdzamy pozostałe kierunki oprócz aktualnego - chcemy znaleźć taki kierunek, że pójście w nim o jeden pixel nie spowoduje sąsiedztwa.
5. Jeżeli nie udało się znaleźć takiego kierunku, to jeżeli nasza łamana nie sąsiaduje jeszcze z żadnym pixelem, to idziemy w tym pierwszym, wylosowanym kierunku i aktualizujemy znacznik sąsiedztwa. Jeżeli łamana już sąsiaduje z pixelem nie należącym do niej, to kończymy generowanie.
6. Nowy kierunek staje się aktualnym
7. Następny pixel wzdłuż aktualnego kierunku staje się aktualnym. Zaznaczamy go jako ścianę.
8. Kontynuujemy postępowanie od punktu 3

Ilość i parametry wrzucanych łamanych do mapy będą ustalane przez użytkownika.

1. Przeszukiwanie mapy

Nie będzie to przeszukiwanie w głąb, ponieważ wracanie po ścieżce, po której się doszło do pixela jest nieefektywne. Dlatego należy szukać najkrótszej drogi do dowolnego nieodwiedzonego pixela. Zauważmy, że w ten sposób przechodzimy całą mapę.

Będą również specjalne zasady, w której robot będzie wybierał sąsiadów pixela, na którym jest, do przejścia. Oczywiście to nie ma większego znaczenia, ponieważ nie istnieją takie zasady, która dla każdego labiryntu dawałaby optymalne przejście mapy (przy założeniu, że robot nie zna mapy).

Stworzymy nowy hipotetyczny graf (w odróżnieniu od grafu, w którym wierzchołkami są pixele), w którym wierzchołkami będą spójne grupy pixeli sąsiadujących, leżących w równej odległości od punktu początkowego (z którego robot zaczyna przeszukiwanie) w metryce maksimum. Wierzchołkami będą więc grupy leżące na koncentrycznych kwadratowych pierścieniach o szerokości jednego pixela. Grupy te muszą być spójne - w szczególności oznacza to, że można przejść robotem całą grupę nie przechodząc przez żaden pixel nie należący do grupy.

Należy zwrócić uwagę, że aby być wierzchołkiem, nie trzeba być maksymalną spójną grupą leżącą na tym samym pierścieniu. Natomiast graf tworzymy tak, że każda maksymalna grupa pixeli o wyżej wymienionych właściwościach składa się z co najwyżej dwóch wierzchołków nowego grafu.

Powyższe wynika z założenia, że robot zawsze przechodzi przez pixele należące do wierzchołka nowego grafu za jednym zamachem (czyli nie schodzi z grupy, dopóki wszystkie jej pixele nie będą odwiedzone, oraz do przejścia grupy potrzebuje dokładnie tyle ruchów, ile jest w grupie pixeli). Dlatego też, jeżeli robot wejdzie na maksymalną spójną grupę nie na jednym z jej końców, to dzieli ja na dwa wierzchołki nowego grafu.

Robot trzyma w swojej pamięci mapę, na których zaznacza odwiedzone pixele oraz ściany, na które się natknął.

Robot postępuje według następującego schematu:

1. Oznacz startowy pixel jako odwiedzony
2. Przesuń się na pierwszy pierścień (robot znajduje się teraz na pierwszym pierścieniu).
3. Wybierz kierunek poruszania się po aktualnym pierścieniu (losowo)
4. Poruszaj się po pierścieniu, oznaczając pixele w pamięci, dopóki nie napotkasz ściany lub odwiedzony pixel (właśnie robot przeszedł przez jeden wierzchołek nowego grafu). Zliczaj checkpointy i zaznaczaj niezabezpieczone checkpointy. Jeżeli znalezione są już wszystkie, kończ postępowanie.
5. Jeżeli sąsiadujący z aktualnym pixelem pixel z pierścienia bardziej zewnętrznego (uwaga na rogi: mają dwóch takich sąsiadów), a w drugiej kolejności bardziej wewnętrznego nie był jeszcze odwiedzony, to przejdź na niego i kontynuuj od punktu 3.
6. Jeżeli był już odwiedzony, to znajdź najbliższy nieodwiedzony pixel i przejdź na niego (jeżeli mamy kilka punktów w tej samej odległości, to dobrze by było wybierać ten leżący bardziej na zewnątrz). Jeżeli się nie udało przejść na wybrany wierzchołek, ponieważ była na nim ściana, to powtórz szukanie i przechodzenie, aż znaleziony pixel będzie wolny, albo aż nie będzie już nieodwiedzonych pixeli, do których można by dojść - wtedy kończ postępowanie.
7. Kontynuuj od punktu 3

Teoretyczne oszacowanie złożoności takiego algorytmu przedstawia się następująco. Każdy pixel będzie przechodzony dokładnie raz, oprócz przesunięć do najbliższego nieodwiedzonego pixela.

Oznaczenia:

n - rozmiar boku mapy w pixelach

p - liczba szukań najkrótszej drogi

p = o(n²), ponieważ mamy o(n²) wierzchołków tego hipotetycznego grafu (ścian oddzielających te wierzchołki, których możemy szukać jest też o(n²)), i dla każdego wierzchołka szukamy drogi co najwyżej raz (bo szukamy do nieodwiedzonego pixela, ale potem on już będzie odwiedzony). Oczekiwana wartość będzie zapewne mniejsza.

Liczba ruchów robota: o(n² + p*n) = o(n³)

Złożoność obliczeniowa: o(n² * p) = o(n⁴)

Możemy także do problemu oszacowania podejść inaczej: zauważmy, że takie przeszukiwanie jest w miarę izomorficzne z przeszukiwaniem w pewnej kolejności w głąb naszego hipotetycznego grafu. Ponieważ liczba jego wierzchołków i krawędzi jest równa o(n²), to chociaż złożoność obliczeniowa dalej wynosi o(n⁴), to udało nam się ograniczyć liczbę ruchów robota do o(n²).

Powstaje pytanie, jaka jest zasadność użycia szukania najkrótszej drogi, które podnosi bardzo złożoność algorytmu (przy przeszukiwaniu w głąb mamy o(n²)), a właściwie nie obniża pesymistycznej ilości ruchów robota. Zależy to od różnicy pomiędzy czasem wykonania jednej operacji obliczeniowej a czasem przesunięcia robota. Jeżeli np. robot jest na komputerze zdalnym, wtedy opłacalne jest minimalizować liczbę ruchów nawet kosztem o(n²) operacji lokalnych w każdym ruchu.

Zadanie jest następujące: mamy zadane dwa punkty na mapie. Mamy znaleźć najkrótszą ścieżkę je łączącą. Ścieżka nie może zawierać pixeli zajętych przez ściany.

Chyba standardowy algorytm w tej sytuacji, będący uproszczoną wersją algorytmu Dijkstry: przeszukiwanie wszerz grafu pixeli, i wpisywanie w każdy wierzchołek długości najkrótszej drogi wiodącej do źródła (początkowego pixela szukanej drogi). Oczywiście długość najkrótszej drogi do źródła dla pewnego pixela jest równa minimalnej długości tej drogi dla sąsiadów pixela (dół, góra, lewy, prawy) plus jeden. Przeszukujemy wszerz, dopóki nie będziemy rozpatrywać pixela docelowego.

Następnie należy uzyskać ścieżkę. W tym celu zaczynamy w punkcie docelowym. Zapamiętujemy go jako koniec ścieżki i ustawiamy jako aktualnego. Teraz wybieramy tego sąsiada aktualnego pixela, który ma najkrótszą drogę do źródła (czyli sprawdzamy, który sąsiad ma najmniejszą wartość poprzednio wyliczonego atrybutu) i ustawiamy go na aktualnego. Wrzucamy go na ścieżkę przed poprzednio wrzuconym pixelem Kontynuujemy, podczas gdy aktualny pixel nie jest źródłem.

Oczywiście całe przeszukiwanie odbywa się na mapie zapamiętanej przez robota. Robot w tym czasie się nie porusza. Złożoność obliczeniowa jest równa o(n²)

Gdy szukamy drogi do najbliższego nieodwiedzonego wierzchołka, robimy podobnie jak poprzednio, tylko przeszukujemy wszerz, gdy nie napotkamy na pierwszy nieodwiedzony pixel. Ponadto najpierw należy sprawdzić 2 sąsiadów: na zewnątrz pierścienia i wewnątrz pierścienia, czy któryś z nich jest nie odwiedzony. W takim wypadku (który będzie dość częstym przy przeszukiwaniu mapy) pomijamy przeszukiwanie wszerz i przesuwamy robota na znaleziony punkt.

1. Znalezienie najkrótszych ścieżek łączących każdą parę checkpointów

Wykonujemy ten krok, aby potem móc znaleźć odpowiednią ścieżkę przechodzenia.

W pewnej kolejności dla każdego checkpointa wykonujemy

1. Wykonujemy przeszukiwanie wszerz, tak jak przy szukaniu najkrótszej drogi: w każdym pixelu zapamiętujemy odległość do aktualnego checkpointa. Kontynuujemy przeszukiwanie, dopóki wszystkie checkpointy za aktualnym nie mają oznaczonej najkrótszej drogi do aktualnego.
2. Dla każdego pixela za aktualnym znajdujemy ścieżkę do aktualnego checkpointa (jak w znajdowaniu najkrótszej drogi) i zapamiętujemy ją.

Złożoność obliczeniowa tego kroku to o(n²q) (q - liczba niezabezpieczonych checkpointów).

2. Aproksymacyjne rozwiązanie problemu komiwojażera dla grafu checkpointów

Ponieważ w ogólności problem komiwojażera jest np-zupełny, stosujemy rozwiązanie aproksymacyjne. Polega ono na:

1. Znalezienie minimalnego drzewa rozpinającego
2. Znalezienie ścieżki, która jest taka, jaka się tworzy przy przeszukiwaniu w głąb tego drzewa.

Skonstruowane drzewo zapamiętujemy.

W praktyce nie będziemy szukali ścieżki poprzez przeszukiwanie w głąb, a potem jej przechodzili, tylko będziemy ją konstruować w trakcie chodzenia robotem.

Zastosujemy algorytm Kruskala. Przedstawia się on następująco:

1. Sortujemy wszystkie krawędzie po wagach, czyli odległościach ich wierzchołków.
2. Inicjujemy zbiór krawędzi drzewa na pusty
3. Wyszukujemy taką krawędź o minimalnej wadze (idąc po kolei po krawędziach w kierunku rosnącym), że graf indukowany ze zbioru krawędzi powiększonego o tą krawędź będzie lasem i dołączamy ją do tego zbioru. W praktyce utrzymujemy dla każdego wierzchołka informację, do którego drzewa z lasu należy. Następnie sprawdzamy, czy wierzchołki tej krawędzi są w różnych drzewach. Jeżeli tak, to dodanie jej nie spowoduje powstania cyklu - wtedy trzeba połączyć te dwie składowe.
4. Powtarzamy postępowanie, aż liczba krawędzi w zbiorze będzie równa ilości wierzchołków grafu powiększonej o jeden (co jest równoważne faktowi, że zostanie dokładnie jedno drzewo w lesie).

Przy tym algorytmie stosuje się specjalną strukturę danych (drzewa z kompresją ścieżek), która pozwala uzyskać złożoność obliczeniową całego algorytmu równą o(q² log q).

1. Przechodzenie przez wszystkie checkpointy, aż któryś zostanie zabezpieczony

Robot aktualnie stoi tam, gdzie go ostatnio zostawiliśmy, czyli na jednym z checkpointów. Rozpoczynamy przeszukiwanie w głąb właśnie od tego checkpointa. Przesuwamy robota po zapamiętanych ścieżkach. Przeszukiwania w głąb nie będę opisywał (patrz "Algorytmy i Struktury Danych", Diks i inni). Można zastosować pewne usprawnienie podczas przeszukiwania (w wersji iteracyjnej): gdy zdejmujemy ze stosu następny checkpoint do przejścia, możemy przejść do niego robotem bezpośrednio (mamy zapamiętaną ścieżkę, a nie wracać po krawędziach, po których przyszliśmy, jak w wersji rekurencyjnej)

Złożoność obliczeniowa tego etapu wynosi o(qn). Robot musi wykonać co najwyżej 2*(suma wag krawędzi minimalnego drzewa rozpinającego) ruchów, czyli o(qn). Gdy w końcu zabezpieczymy jeden z checkpointów, zapamiętujemy ten fakt, i przystępujemy do następnej fazy.

2. Sprowadzenie poprzedniego rozwiązania do nowej sytuacji

Teraz potrzebujemy powtórzyć postępowanie z poprzedniego punktu: przejść wszystkie niezabezpieczone checkpointy. Musimy znaleźć w miarę minimalną ścieżkę, przechodzącą przez wszystkie rozpatrywane checkpointy (czyli te co poprzednio oprócz ostatnio zabezpieczonego). Sztuka polega na tym, aby wykorzystać rozwiązanie dla poprzedniego grafu.

Usunięcie tego checkpointa z minimalnego drzewa rozpinającego spowodowało rozspójnienie drzewa. Mamy teraz pewną ilość spójnych składowych, które trzeba połączyć. Więc teraz potraktujemy je jako wierzchołki nowego grafu, w którym będziemy szukać minimalnego drzewa rozpinającego. Wagami krawędzi między dwiema składowymi będzie minimalna waga krawędzi łączących te dwie składowe (czyli krawędzi incydentnych z wierzchołkami jednocześnie z jednej i drugiej składowej).

W wyniku znalezienia tego drzewa jesteśmy w stanie skonstruować nowe drzewo rozpinające grafu niezabezpieczonych checkpointów złożone z krawędzi poprzedniego drzewa checkpointów pomniejszonego o zabezpieczony wierzchołek, a powiększonego o krawędzie grafu checkpointów odpowiadające krawędziom minimalnego drzewa rozpinającego spójnych składowych, znalezionego w poprzednim kroku.

Aby podzielić drzewo na składowe, wykonujemy przeszukiwanie w głąb, zapamiętując dla każdego wierzchołka, do której składowej należy. Potem dla każdej pary wierzchołków z różnych składowych sprawdzamy, czy zapamiętana odległość składowych jest mniejsza od wagi aktualnej krawędzi, i ewentualnie ją aktualizujemy. Na początku odległości między składowymi inicjalizujemy na +nieskończoność.

Ogólnie złożoność obliczeniowa tej fazy wynosi o(u² * log u + q²), gdzie u to liczba składowych, na które dzieli się minimalne drzewo rozpinające po usunięciu ostatnio zabezpieczonego wierzchołka.

3. Podsumowanie

Możemy spróbować oszacować złożoność q-krotnego powtarzania kroku 6, czyli sprowadzania minimalnego drzewa rozpinającego dla coraz mniejszej liczby wierzchołków. Złożoność pojedynczego kroku tej fazy jest o(u² * log u + q²). Składnik q² nie będzie się istotnie zmieniał, więc po q-krotnym wykonaniu otrzymamy o(q³), natomiast rozważenia wymaga całkowita liczba składowych, które trzeba rozważyć. Pesymistycznie, każde usunięcie jednego checkpointa z drzewa może stworzyć graf izolowanych wierzchołków. Wtedy mamy całkowity koszt o(q³ * log q). Jednak ze względu na specyfikę grafu checkpointów (np. dla każdych trzech parami różnych wierzchołków jest spełniona nierówność trójkąta) wydaje mi się, że czas oczekiwany będzie mniejszy.

Złożoność obliczeniowa całego algorytmu chodzenia robota przedstawia się następująco: o(n⁴ + k³ * log k). Przy założeniu, że liczba checkpointów jest proporcjonalna do długości boku mapy, mamy ostateczną złożoność pesymistyczną o(n⁴).

Liczba ruchów robota można ograniczyć przez o(n² + k²n). I tutaj oczekiwana ilość przesunięć powinna być mniejsza. Dla liczby checkpointów o(n), mamy ilość ruchów robota o(n³).

Struktury danych

1. Klasy

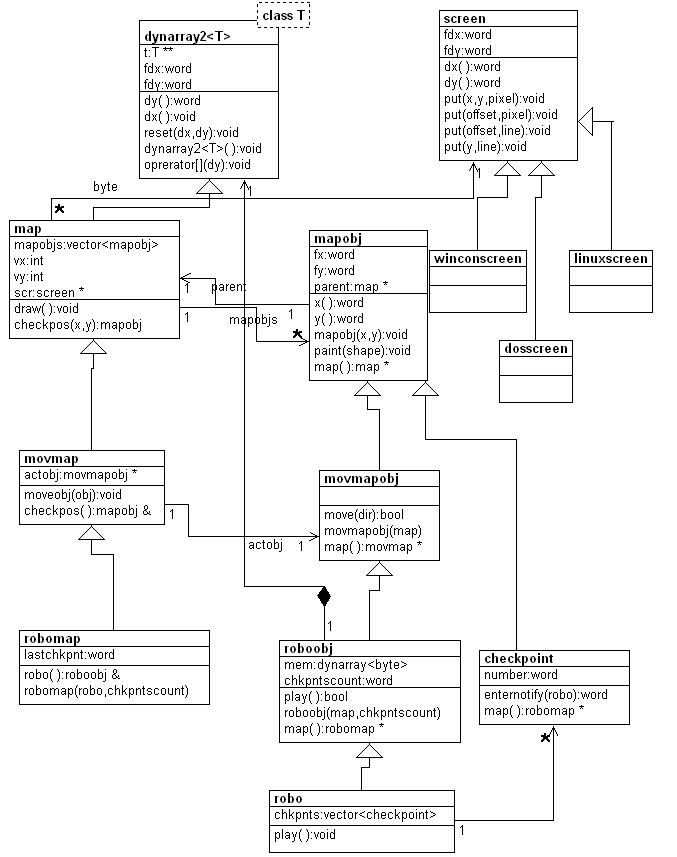
Podstawowe klasy to:

1. dynarray2<T> - template'owa klasa ukrywająca dynamicznie alokowalną tablicę dwuwymiarową elementów o typie T
2. dynhalfarray2<T> - template'owa klasa podobna do dynarray2, tyle, że przechowuje tylko dolny trójkąt macierzy (bez diagonalii)
3. vector<T> - template'owa klasa ukrywająca dynamicznie alokowany wektor elementów danego typu
4. queue<T> - template'owa klasa ukrywająca kolejkę FIFO
5. stack<T> - template'owa klasa zapewniająca operacje na stosie, dziedziczy po vector<T> (implementacja tablicowa)
6. mintreedata - klasa zapewniająca operacje find i union na zbiorach potrzebna przy znajdowaniu drzewa minimalnego rozpinającego graf.
7. tree - klasa zapewniająca przechowywanie struktury drzewa w pamięci.
8. map - reprezentuje podstawową mapę o pewnym rozmiarze. Zapewnia trzymanie pewnych obiektów mających określoną pozycję oraz rysowanie mapy oraz tych obiektów na ekranie. Tylko jedna warstwa - na danym pixelu może być co najwyżej jeden obiekt..
9. mapobj - podstawowy typ dla obiektów mogących znaleźć się na mapie. Każdy mapobj ma swoją pozycję i wygląd.
10. movmap - mapa, po której pewne obiekty mogą się poruszać. Posiada aktywny obiekt, który jest zawsze widoczny na ekranie. Zapewnia drugą warstwę, na której znajduje się ten zawsze widoczny obiekt.
11. movmapobj - movobj, który może się poruszać się po mapie.
12. screen - klasa zapewniająca usługi związane z rysowaniem. Zakładam implementację w trybie tekstowym (0x03)(80x50), ale można (po zmianie typu screen::attr) również w trybie graficznym.
13. robomap - movmap, która oprócz poprzednich usług zajmuje się zatrzaskiwaniem checkpointów.
14. roboobj - podstawowa klasa robota, który próbuje znaleźć checkpointy. Wie, jaka jest liczba checkpointów na mapie
15. checkpoint - mapobj, który posiada swój numer oraz da się zabezpieczyć
16. robo - właściwa klasa z algorytmem robota.

Rysunek znajdujący się poniżej prezentuje podstawowe relacje pomiędzy klasami. Nie należy brać atrybutów tych klas uwidocznionych na rysunku uważać za wiążace. Wiążace są definicje klas.

Dalej są definicje klas (w C++). Nie ma deklaracji wszystkich funkcji składowych - są tylko ważne dla modelu (mające znaczenie dla powiązań między klasami i obiektami). Inne należy dodać samemu.

class vector<T> {

private:

class dynarray2<T> {

private:

class mapobj;

class map : protected dynarray2<word>

protected:

class mapobj {

friend map;

class movmap : public map {

protected:

public:

class robomap : public movmap {

private:

class roboobj : public movmapobj {

protected:

class checkpoint : public mapobj {

private:

class robo : public roboobj {

private:

class map::plotter {

private:

class screen {

private:

1. Drzewo z dowiązaniami do ojca i kompresją ścieżek

Ta struktura jest wykorzystywana przy znajdowaniu minimalnego drzewa rozpinającego. Jej celem jest efektywne przechowywanie pewnych elementów podzielonych na zbiory, szybkie wyszukiwanie, czy dwa elementy należą do tego samego zbioru, i szybkie łączenie dwóch zbiorów w jeden.

class mintreedata {

private:

struct node {

word parent; //to jest indeks w tablicy nodes, gdzie jest ojciec tego elementu

};

vector<word> sizes; // rozmiary zbiorów

vector<node> nodes;

public:

void init(word count); // tworzy count nodeów w oddzielnych zbiorach, które otrzymują kolejne numery (od zera), alokuje i ustawia sizes na 1,

word find(word data); // znajduje setid

void union(word setid1, word setid2);

};

 

void mintreedata::init(word count);

Alokuje count node'ów w nodes, ustawia ich parent na 0xFFFF. Alokuje count wordów w sizes, ustawia każdy element na 1.

word mintreedata::find(word data);

Zwraca pewną liczbę jednoznacznie identyfikującą zbiór, do którego należy node o kluczu data. Odbywa się do w dwóch przebiegach: najpierw idziemy kolejno po nodach, zaczynając od node[data], potem node[node[i].parent] itd., aż do node'a takiego, że node[i].parent == 0xFFFF. Wtedy indeks tego node'a jest identyfikatorem zbioru.

W drugim przebiegu zaczynamy znowu od node[data] itd., i ustawiamy każdemu node'owi parenta na indeks tego node'a na poprzedniej ścieżce, którego parent == 0xFFFF.

void mintreedata::union(word setid1, word setid2);

Ta funkcja łączy dwa zbiory. Ściśle rzecz biorąc podłącza szczytowy node mniejszego z tych zbiorów do szczytowego node'a większego (node jest szczytowy, gdy jego parent == 0xFFFF, dla każdego zbioru istnieje dokładnie jeden node szczytowy należący do niego).

Na początku sprawdzamy rozmiary zbiorów w tablicy sizes - będą to sizes[setid1], sizes[setid2]. Dla ustalenia uwagi załóżmy że podłączamy setid2 pod setid1. Więc wystarczy wykonać nodes[setid2].parent = setid1. Potem trzeba jeszcze zaktualizować rozmiar w tablicy sizes.

Złożoność operacji union jest o(1), a find o(n log*n), gdzie log*n jest funkcją odwrotną do funkcji Ackermanna. Inicjalizacja w czasie liniowym.

2. Listowa reprezentacja drzewa

W trakcie postępowania musimy pamiętać drzewo. Można w tym celu użyć zwykłej reprezentacji listowej, jednakże ze względu na liniową ilość krawędzi można to zrobić nieco sprawniej.

Implementacja listy jest na tablicy edges. Koniec jest zaznaczony przez 0xFFFF. Utrzymywana jest lista nieużywanych elementów na jej początek wskazuje firstempty. Na początku wszystkie elementy powinny się znajdować na tej liście. Potem, w miarę dodawania nowych krawędzi, zdejmujemy z listy pustych elementów pierwszy z nich i dodajemy go na początku wybranej listy sąsiedztwa.

Każdy wierzchołek ma przechowywane początek listy. Jest to indeks w tablicy edges pierwszego sąsiada. Te dane są przechowywane w tablicy firstedges. Wartość 0xFFFF oznacza, że nie ma sąsiada.

Operację wstawiania już opisałem, usuwamy według wszelkich reguł list jednokierunkowych, zwolniony element tablicy edge należy podłączyć na początku listy pustych elementów.

Jeżeli kasujemy wierzchołek, to należy podłączyć całą jego listę sąsiedztwa na początku listy pustych elementów, a wcześniej trzeba usunąć go z list sąsiedztwa wszystkich jego sąsiadów.

Uwaga - będziemy rozpatrywać drzewo nieskierowane, więc jeżeli dodajemy krawędź {a, b}, to należy wykonać insedge(a, b); insedge(b, a). Tak samo przy usuwaniu krawędzi.

Program główny będzie wyglądał tak:

1. Stworzenie obiektu klasy pochodnej od screen, i odpowiednia jego inicjalizacja (obiekt powinien być globalny)
2. Inicjalizacja ekranu.
3. Wczytanie rozmiarów planszy i liczby checkpointów
4. Stworzenie obiektu mapy (lokalnie) i jego inicjalizacja.
5. Wczytywanie parametrów generowania krzywych z klawiatury oraz ilości krzywych do wygenerowania z tymi parametrami oraz tylu krotne wywołanie funkcji mar::generatepoly, aż znudzi się użytkownikowi. Użytkownik powinien widzieć mapę po wykonaniu każdej serii generacji i mieć możliwość rozpoczęcia od nowa.
6. Wczytywanie ilości losowych ścian do wygenerowania i ich generowanie funkcją map::generatewall, aż się znudzi użytkownikowi.
7. Wygenerowanie odpowiedniej liczby checkpointów przy użyciu funkcji robomap::generatecheckpoint, ewentualna aktualizacja liczby checkpointów, gdy nie udało się wygenerować żądanej ich liczby.
8. Stworzenie obiektu klasy robo i jej zainicjalizowanie
9. Wywołanie funkcji robo::play i wyświetlenie odpowiedniego komunikatu w zależności od zwróconej wartości.
10. Zamknięcie ekranu

A tutaj mamy funkcję robo::play.

1. Wywołujemy funkcję searchmap. Jeżeli nie udało się znaleźć wszystkich checkpointów, zwracamy false i wychodzimy z funkcji
2. Sprawdzamy, czy wszystkie checkpointy są już zabezpieczone, jeżeli tak, wychodzimy z funkcji z wartością true.
3. Wywołujemy robo::findpaths
4. Wywołujemy robo::findmintree
5. W pętli nieskończonej: przechodzimy drzewo checkpointów używając funkcji robo::traversetree, jako parametr podając ostatnio odwiedzony wierzchołek; na początku będzie to ostatni z niezabezpieczonych checkpointów, potem kolejny zabezpieczony checkpoint, którego numer zwraca robo::traversetree. Jeżeli wszystkie checkpointy są zabezpieczone, to wychodzimy z funkcji z wartością true. W przeciwnym wypadku wywołujemy domintree, jako parametr podając to, co zwróciła robo::traversetree. Skaczemy do początku pętli.

1. Format przechowywania mapy

Mapa jest przechowywana w obiektach klasy map w postaci dwuwymiarowej tablicy elementów typu word. Każdy z takich elementów trzyma informację o jednym pixelu. Wartość 0 oznacza wolne nieodwiedzone pole, 1 ścianę, 2 puste odwiedzone pole, zaś każda większa wartość oznacza, że na tym polu jest jeden obiekt 0 - to implikuje, że to pole było już odwiedzone. W tym wypadku po odjęciu od wartości 3 otrzymujemy indeks w tablicy map::mapobjs, pod którym przechowywany jest ten obiekt znajdujący się na tym polu, który ma najmniejszy indeks w tej tablicy. Mapa ma maksymalne rozmiary 32000 na 32000 pixeli. Maksymalna liczba checkpointów również wynosi 32000.

 

2. Generowanie mapy

Na początku zerujemy mapę i otaczamy ścianami.

Proces generowania łamanych będzie ukrywać funkcja:

void map::generatepoly(word vertprob, /* odpowiada prawdopodobieństwu końca krawędzi - podajmey liczbę dziesięciotysięcznych żądanego prawdopodobieństwa. (p = vertprob/10000)*/

word orientprob, /* odpowiada prawdopodobieństwu kierunku innego niż orientacja - podajmey liczbę dziesięciotysięcznych żądanego prawdopodobieństwa. (p = vertprob/10000)*/

bool orientclockwise /* jeżeli true, to orientacja zgodna z kierunkiem ruchu wskazówek zegara */

);

Treść funkcji jest opisana w sekcji Algorytmy.

Losowe ściany wstawia funkcja

void map::generatewall();

Po prostu losuje pozycję na mapie, i jeżeli na niej nie ma ściany, to ją ustawia.

 

3. Przeszukiwane mapy

Robot przechowuje swoją mapę (robo::mem), która jest czterokrotnie większa od oczekiwanych rozmiarów mapy. Dla każdego pixela jest przechowywana wartość typu byte. Wartość 0 oznacza nieodwiedzone pole, wartość jeden ścianę, wartość 2 odwiedzone pole. Na początku tablica mem powinna być wypełniona zerami.

Przeszukiwanie mapy odbywa się w funkcji:

Funkcja ta zwraca true, gdy znaleziono wszystkie checkpointy i false, gdy nie udało się ich znaleźć mimo przeszukania całej mapy. Postępuje według algorytmu z sekcji przeszukiwanie mapy.

W trakcie swego działania funkcja wywołuje funkcję

która znajduje najbliższy nieodwiedzony pixel, zwraca do niego ścieżkę w zmiennej co i zwraca true, gdy udało się ją znaleźć.

Również użyteczna będzie funkcja

która przesuwa robota wzdłuż podanej ścieżki. Jeżeli w którymś momencie przeszkodziła ściana, to zwraca false. Ścieżkę należy usunąć, jak już będzie niepotrzebna, przez wywołanie reset(0). Funkcja ta przesuwa robotem używając funkcji move.

Funkcja searchmap powinna zapamiętać znalezione niezabezpieczone checkpointy w tablicy chkpnts oraz ustawić ilość niezabezpieczonych checkpointów.

Na samym początku sprawdzamy dwóch sąsiadów naszego wierzchołka, czy nie są puste i nie odwiedzone. W takim wypadku wybieramy jeden z nich, jak w algorytmie, i zwracamy do niego ścieżkę.

Na początku tworzymy kolejkę FIFO przechowującą pozycje pixeli (y, x) i wstawiamy pozycje aktualnego pixela. Kolejka musi pomieścić maksymalnie 8*max(rozmiar mapy pionowy lub poziomy)+4. Tworzymy dodatkową tablicę delta o takich rozmiarach jak robo::mem i wartościach word. Inicjalizujemy ją na wartość 0xFFFF. W punkcie odpowiadającym aktualnym współrzędnym wstawiamy 0. Poprzez wartość 0xFFFF oznaczamy wierzchołek, który jeszcze nie był w kolejce.

Następnie powtarzamy dopóki kolejka nie jest pusta:

1. Pobieramy element z kolejki.
2. Jeżeli aktualny pixel jest nieodwiedzony - czyli taki, jakiego szukamy - wychodzimy z pętli.
3. Wstawiamy wszystkich bezpośrednich sąsiadów aktualnego pixela nie będących ścianami i mających wartość delta równą 0xFFFF lub większą od delta(x, y)+1 na kolejkę oraz ustawiamy dla nich wartość w tablicy delta na delta(x, y)+1.

Po wyjściu z tej pętli albo dostaniemy najbliższy nieodwiedzony pixel (on będzie aktualnym), albo okaże się, że kolejka jest pusta i wtedy wychodzimy z funkcji zwracając false.

Jeżeli dostaliśmy pixel, to teraz musimy skonstruować do niego drogę. Znamy jej długość, więc rezerwujemy odpowiednią ilość elementów w parametrze co.

Teraz będziemy wracać do punktu początkowego, zapamiętując ścieżkę od tyłu. Na początku pewien indeks wskazuje na ostatni element tablicy co, a potem po każdym obrocie pętli będzie on dekrementowany.

Poprzednika pewnego pixela leżącego na szukanej ścieżce będziemy identyfikować po minimalnym atrybucie delta. Inaczej mówiąc, szukamy tego z sąsiadów bezpośrednich, który ma najmniejszą wartość delta, kierunek, w jakim trzeba iść z tego pixela do aktualnego zapamiętujemy w tablicy co, i zmieniamy pixel aktualny na ten nowy, minimalny. Postępujemy tak, aż aktualny pixel będzie miał delta = 0.

Powyższe postępowanie zamykamy w funkcji

t jest tą pomocniczą tablicą, (y, x) pozycją znalezionego pixela, a w parametrze co funkcja powinna zapamiętać ścieżkę.

Wychodzimy z funkcji z wartością true.

1. Znajdowanie najkrótszych ścieżek między wszystkimi checkpointami

Będzie to robić funkcja

Wypełnia ona tablicę paths odpowiednimi danymi.

Na początku należy ustawić rozmiar tablicy paths na równy ilości znalezionych niezabezpieczonych checkpointów. Trzeba również stworzyć tablicę delta jak w sekcji Znajdowanie najbliższego nieodwiedzonego wierzchołka. W tablicy paths przechowujemy najkrótsze ścieżki między checkpointami. W elemencie (i, j) tej tablicy znajduje się ścieżka od checkpointa, który ma indeks i w tablicy robo::chkpnts do checkpointa o indeksie j.

Dla każdego checkpointa o indeksie w tablicy chkpnts różnym od zera będziemy postępować następująco:

1. Przeszukujemy wszerz jak w sekcji Znajdowanie najbliższego nieodwiedzonego wierzchołka, tyle, że nie wychodzimy, gdy pixel jest nieodwiedzony. Natomiast sprawdzamy w tamtym miejscu, czy aktualny pixel jest checkpointem o indeksie mniejszym od aktualnego. Jeżeli tak, to zwiększamy o jeden pewien counter, początkowo zainicjalizowany na 0. Jeżeli counter jest równy indeksowi aktualnego checkpointa zwiększonemu o jeden (i+1), to wychodzimy z przeszukiwania wszerz.
2. Dla każdego checkpointa o indeksie mniejszym od i wywołujemy genpath z pozycją tego checkpointa oraz odpowiednią ścieżką z tablicy paths

Zauważmy, że możemy traktować rozmiar tablicy paths[i][j] jako odległość między checkpointem i a j.

No i to już koniec. Zwalniamy tymczasową pamięć i wychodzimy z funkcji. Tablica mem będzie już niepotrzebna.

1. Znajdowanie minimalnego drzewa rozpinającego

W funkcji

void robo::findmintree();

szukamy minimalnego drzewa rozpinającego algorytmem Kruskala. Do przechowywania informacji o spójnych zbiorach wierzchołków używamy struktury opisanej wcześniej. Potrzebujemy również posortować wszystkie krawędzie. W rzeczywistości będziemy sortować pary liczb określające początkowy i końcowy checkpoint - wszak możemy dla nich otrzymać klucz - czyli odległość. Wrzucamy wszystkie podzbiory dwuelementowe zbioru {1, ..., liczba niezabezpieczonych checkpointów} do wektora, sortujemy quicksortem (z medianą z trzech i nie tym wbudowanym w C++, bo to kosztowna część algorytmu).

Właściwa implementacja powinna się znaleźć w funkcji

struct robo::edge {

word source;

word dest;

};

void robo::kruskal(word count, const vector<edge> &edges, const dynhalfarray<edge> *trans, tree &t);

count to liczba wierzchołków grafu, w edges mamy posortowane krawędzie grafu, trans jest wskaźnikiem na macierz przekształceń krawędzi (będzie potrzebne później - jeżeli przekazane jest 0, to nie ma żadnej translacji), zaś t to wynikowe drzewo - do niego algorytm powinien dodawać krawędzie drzewa. Funkcja powinna założyć, że drzewo jest już zainicjalizowane.

Tworzymy obiekt klasy mintreedata i inicjalizujemy na liczbę niezabezpieczonych checkpointów. No i teraz mając to wszystko możemy postępować według stosownego algorytmu opisanego w części algorytmu.

Jeżeli znaleźliśmy już krawędź należąca do drzewa, to dokonujemy translacji (jeżeli trans != 0). Chodzi o to, aby w drzewie połączyć inne wierzchołki niż te, które wynikają z edge'a w tablicy edges. Więc jeżeli {a, b} to krawędź znaleziona w tablicy edges, b<a, i spełnia założenia krawędzi co do dodania do drzewa, to do t wsadzamy krawędź {trans[a][b].source, trans[a][b].dest}. Jeżeli trans==0, to wsadzamy po prostu {a, b}.

Funkcja robo::findmintree powinna wywoływać funkcję robo::kruskal z parametrem trans równym zero. Pozostałe struktury powinna ona stworzyć, jak również powinna posortować krawędzie według wag.

2. Przechodzenie drzewa

word robo::traversetree(word chkpnt);

Jak już pisałem wcześniej, przechodzimy drzewo w głąb. W tym celu potrzebujemy stos (rekurencyjne wywołania funkcji składowych zajmują 8 bajtów plus parametry). Przecież stos można łatwo zrobić na tablicy wordów o rozmiarze równym liczbie wierzchołków. Oprócz tego musimy pamiętać dla każdego wierzchołka, czy był już na stosie - w wektorze wordów o nazwie visited.

Jeżeli stos lub tablica visited ma rozmiar równy zero, to ustawiamy odpowiedni (równy ilości rozpatrywanych checkpointów).

Na początku inicjalizujemy wektor visited na 0. Przechodzenie zaczynamy od podanego checkpointa. Wrzucamy go na stos, i aktualizujemy wektor visited.

No a teraz to już jak to przechodzenie w głąb - zdejmujemy checkpointa ze stosu przechodzimy tam robotem (używając gotopath i tablicy paths), jeżeli go zabezpieczyliśmy, to wychodzimy z pętli, zwracając jego indeks w tablicy chkpnts.

Teraz musimy dodać wszystkich nieodwiedzonych i nie będących jeszcze na stosie sąsiadów zdjętego wierzchołka na stos - przechodzimy po kolei listę sąsiedztwa dla naszego wierzchołka i aktualizujemy wektor visited po wrzuceniu checkpointa na stos. Powtarzamy całość, dopóki nie zabezpieczymy sobie jakiegoś checkpointa.

Przed wyjściem z funkcji nie usuwamy stosu, drzewa ani tablicy visited.

3. Sprowadzanie drzewa do nowej sytuacji

void robo::domintree(word chkpnt);

Najpierw usuwamy wierzchołek z drzewa. Teraz musimy oznaczyć spójne składowe. W tym celu przechodzimy graf w głąb. Tym razem trochę inaczej. W pętli. Używamy znowu stos i wektor visited. Tym razem w visited przechowujemy id składowej. Wartość 0xFFFF oznacza nieodwiedzony wierzchołek. Na ta wartość inicjalizujemy ten wektor.

I teraz kolejno dla każdego wierzchołka: jeżeli jest on nieodwiedzony, to: ustaw numer aktualnej składowej na równy dotychczasowej liczbie znalezionych składowych, zwiększ liczbę składowych o jeden, dla tego wierzchołka wykonaj przeszukiwanie w głąb.

Podczas przeszukiwania nie chodź robotem, ale ustawiaj wartości w tablicy visited na numer aktualnej składowej wtedy, gdy ją aktualizowałeś. Nie wyskakuj z przechodzenia - przechodź, dopóki stos nie będzie pusty.

Po zakończeniu przechodzeniu wróć do pętli i szukaj znowu nieodwiedzonego wierzchołka. Oczywiście nie należy inicjalizować znowu tablicy visited.

I już. Mamy podzielony graf.

Teraz odległości między składowymi. Tworzymy dwie półtablice dwuwymiarowe - jedna typu word - tam będą odległości między składowymi, a druga typu robo::edge - tu będą krawędzie odpowiadające tym odległościom łączące dwie składowe o numerach odpowiadających wierszowi i kolumnie. Każda z tych tablic powinna mieć wymiary równe liczbie składowych.

Mając te tablice, przeglądamy wszystkie krawędzie (tj. całą tablicę paths), sprawdzamy, do jakich składowych należą końce aktualnej krawędzi, jeżeli do różnych, to sprawdzamy, czy długość ścieżki jest mniejsza od wagi krawędzi łączącej odpowiednie składowe w tablicy odległości składowych. Jeżeli tak, to aktualizujemy tą wartość i krawędź w tablicy krawędzi.

Następnie wywołujemy robo::kruskal dla grafu składowych - najpierw musimy posortować krawędzie łączące składowe po wagach - tworzymy wektor i quicksort. Jako parametr trans przekazujemy naszą tablicę krawędzi, jako drzewo obiekt, który dotychczas był drzewem.

4. Implementacja pozostałych funkcji

vector<T>

T *t;

Trzyma wskaźnik na dynamiczną tablicę.

word s;

Zawiera rozmiar tablicy.

void reset (word size);

Ustala nowy rozmiar tablicy na size, kasuje poprzednie dane.

void resize (word size);

Ustawia nowy rozmiar, dane są kopiowane.

vector () : t(0), s(0) {}

Inicjalizuje zmienne składowe na 0.

vector(word size): t(0) { reset(size); }

Inicjalizuje rozmiar tablicy na size.

~vector() { delete [] t; }

Usuwa tablicę.

word size() const { return size; }

Zwraca rozmiar tablicy.

T &oprerator[](word i) const { return const_cast<T&>(t[i]); }

operator T*() const { return const_cast<T&>(t); }

Operatory ułatwiające użycie tablicy. W przypadku kompilatorów bez operatora const_cast należy zastosować zwykłe rzutowanie.

dynarray2<T>

T ** t;

Trzyma tablicę wskaźników na pierwsze elementy wierszy tablicy. t==0 oznacza pustą tablicę.

word fdx;

word fdy;

Przechowują rozmiary tablicy.

dynarray2() : t(0) {}

dynarray2(word dy, word dx);

Inicjalizują tablicę.

~dynarray2() { if (t) delete t[0]; delete t; }

Zwalnia pamięć przeznaczoną ta tablicę. Najpierw musi zwolnić pamięć zaalokowaną na trzymanie elementów tablicy (wskaźnik na ta tablicę jest przechowywany w t[0] (jeżeli t nie jest 0)). Następnie musi zwolnić tablicę wskaźników na pierwsze elementy wierszy.

void alloc(word dy, word dx);

Alokuje pamięć pod tablicę o rozmiarach dy wierszy na dx kolumn. Na początku należy zaalokować dy wskaźników na T, i przypiąć adres tej pamięci to zmiennej składowej t. Następnie należy zaalokować dx*dy elementów typu T, i adres przypisać to t[0]. Teraz trzeba wpisać adresy w wektor t. W pętli dla i od 1 do dy-1 ustawiamy t[i] na t[i -1] + dx.

word dy () const { return fdx; }

void dx () const { return fdy; }

Zwracają rozmiary tablicy.

void reset (word dy, word dx);

Ustawia nowy rozmiar, wszystkie poprzednie dane są tracone. Najpierw dealokuje pamięć zaalokowaną poprzednio, a potem używa alloc.

void resize (word dy, word dx);

Ustawia nowy rozmiar, dane są kopiowane. Tworzy tymczasową zmienną, aby przechować t, wywołuje alloc, a następnie kopiuje zawartość poprzedniej tablicy linia po linii, tak, że każda linia starej tablicy jest w innej linii nowej tablicy. Na końcu trzeba zwolnić pamięć poprzedniej tablicy.

T* oprerator[](word dy) const;

operator T**() const;

T& operator()(dword offset) const;

Operatory ułatwiające dostęp do danych.

 

dynhalfarray2<T>

To samo co dynarray2, tyle, że tylko dolny trójkąt macierzy, bez diagonalii. Trzeba zmienić pętlę w alloc, tak aby ustawiała odpowiednie adresy. I należy alokować odpowiednią ilość pamięci.

map

vector<mapobj *> mapobjs;

Lista obiektów na mapie.

word sx;

word sy;

word sdx;

word sdy;

Pozycja i rozmiar okna wyświetlanego na ekranie.

word vx;

word vy;

Pozycja na mapie pierwszego widocznego pixela na ekranie.

screen * scr;

Wskaźnik na ekran, na którym ma być wyświetlana mapa.

class plotter;

Klasa rysująca mapę na ekranie.

map() : scr(0) {}

Konstruktor domyślny.

map(word dx, word dy, screen *s)

Ustawia ekran na podany oraz ustawia rozmiary tablicy na podane. Otacza mapę ścianami.

~map();

Dealokuje pamięć przeznaczoną na mapobje.

inline void insobj(mapobj *);

Dodaje nowo zaalokowany dynamicznie mapobj do listy. Dealokacją pamięci zajmie się obiekt map. Tylko dynamicznie zaalokowane obiekty!

inline void delobj(mapobj *);

Usuwa podany obiekt z mapobjs i dealokuje pamięć.

void draw();

Rysuje mapę na podanym ekranie. Wykonuje to poprzez w pętli stworzenie tymczasowego obiektu klasy map::plotter i wywołania funkcji screen::put(word, word, word, map::plotter) dla każdego wiersza z odpowiednimi parametrami, tak aby mapa wyświetliła się w oknie określonym przez zmienne sx, sy, sdx, sdy od miejsca vx, vy. Te parametry to sy+numer_wiersza_okna, sx, sdx. Obiekt klasy map::plotter musi mieć przekazany parametr offset równy (vy + numer_wiersza_okna)*dx + vx, np.:

scr->put(sy + i, sx, sdx, plotter(this, (vy+i)*dx+vx));

inline void setclip(word sy, word sx, word sdy, sdx);

Ustawia zmienne sy, sx, sdy, sdx. Nie przerysowuje mapy ani jej nie kasuje.

inline void setpos(word vx, word vy);

Ustawia zmienne vx, vy. Nie przerysowuje mapy ani jej nie kasuje.

inline screen::attr getattr(dword offset);

Zwraca atrybuty pixela o podanym offsecie na mapie (offset to kolejny numer pixela, pixel o pozycji y, x na mapie ma offset równy y*dx+x). Ta funkcja uwzględnia mapobje. Kolory i znaki do ustalenia przez implementatora.

mapobj

word fx;

word fy;

Przechowują pozycję mapobja na mapie.

map &parent;

Mapa, na której znajduje się obiekt. Nie można jej zmienić.

void mapobj (word x, word y, map &parent) : fx(x), fy(y), parent(parent) {}

Jedyny konstruktor obiektu. Ustawia odpowiednie zmienne.

virtual ~mapobj()

Wirtualny destruktor, ponieważ obiekty będą niszczone jako mapobje.

word x() { return fx; }

word y() { return fy; }

Funkcje dające dostęp do pozycji mapobja.

virtual attr paint() =0;

Wirtualna funkcja, która zwraca wygląd obiektu.

map &map() const;

Pozwala na dostęp do mapy, na której znajduje się obiekt. Nie powinno się w obiektach, które dziedziczą po mapobj, używać zmiennej parent. Należy używać tej funkcji.

movmap

mapobj* actobj;

Wskaźnik na obiekt, który powinien być zawsze widzialny. Jednocześnie reprezentuję on drugą warstwę - może on być na polu z innym mapobjem. Wtedy on jest widzialny, a nie obiekt pod nim.

enum direction { up, right, down, left };

Ten typ reprezentuje kierunek, w jaki się może poruszyć movmapobj.

~movmap() ;

Jego zadaniem jest dealokacja pamięci actobja.

bool adjust();

Zapewnia, że actobj jest widzialny, poprzez ustawienie odpowiednie zmiennych vx i vy. Powinno być tak, że jeżeli actobj znajduje się za blisko od którejś krawędzi okna ekranowego (tj. bliżej niż delta), to należy ustawić na wartości najmniej różniące się od aktualnych, ale takie, aby actobj był w odległości delta od krawędzi. Zwraca true, gdy vx lub vy się zmieniło.

void setactobj(mapobj *actobj);

Ustawia actobj.

bool moveobj(movmapobj *, direction dir);

Porusza podanym obiektem w danym kierunku, zmieniając jego współrzędne. Jeżeli nie jest to obiekt z drugiej warstwy, to trzeba uaktualnić tablicę przechowującą mapę oraz sprawdzić, czy nie będzie dwóch obiektów na jednym polu. Wywołuje adjust, jeżeli podany obiekt jest actobjem; jeżeli zwróciło true, to przerysowuje całą mapę. W przeciwnym wypadku aktualizuje rysunek na ekranie poprzez przerysowanie dwóch zmienionych pixeli. Zwraca true, gdy poruszenie się udało.

Ta funkcja powinna również opóźniać wykonanie programu tak, aby użytkownik mógł obserwować ruch robota na ekranie. Opóźnienie powinno być ustawialne z klawiatury właśnie w trakcie trwania tej pauzy. Czas pauzy nie powinien zależeć od szybkości komputera, co wymusza korzystanie z zegara. Można do tego użyć np. funkcji GetTickCount z Windows API lub obiektu klasy Timer z biblioteki Borland C++ 3.1.

mapobj *checkpos(mapobj *) const;

Zwraca obiekt pierwszej warstwy, który jest na tym polu, co argument, lub 0. W szczególności dla obiektów pierwszej warstwy zwraca podany argument. Po prostu zagląda do odpowiedniej komórki tablicy przechowującej mapę, a następnie do tablicy mapobjs.

virtual void draw();

Najpierw wywołuje map::draw, a potem rysuje actobj - czyli drugą warstwę w odpowiedniej pozycji w oknie na ekranie.

movmapobj

movmapobj(word x, word y, movmap *parent) : mapobj(x, y, parent) {}

Jedyny konstruktor. Przekazuje do mapobj odpowiednie wartości. Należy zwrócić uwagę, że movmapobj może być tylko na mapie movmap.

movmap &map () const { return static_cast<movmap &>(parent); }

W związku z tym możemy spokojnie przedefiniować funkcję map, aby zwracała referencję do movmapa, konwertując statycznie zmienną map. Jeżeli kompilator nie wspiera operatora static_cast, używamy zwykłego rzutowania.

typedef movmap::direction direction;

Aby było wygodniej, definiujemy typ direction w movmapobj.

bool move(direction dir) { return map().moveobj(this, dir); }

Porusza obiektem używając movmap::move, jeżeli udało się ruszyć, i tylko wtedy, zwraca true; przerysowuje mapę.

mapobj *checkpos() const { return map().checkpos(this); }

Zwraca mapobj, który znajduje się w pierwszej warstwie na aktualnej pozycji lub 0. Używa map::checkpos.

robomap

word secchkpntcount;

Przechowuje liczbę zabezpieczonych checkpointów.

word chkpntscount;

Przechowuje liczbę wszystkich checkpointów.

void checkednotify(checkpoint *);

Ta funkcja powinna być wywoływana po zabezpieczeniu checkpointa, implementacja aktualizuje zmienne składowe, tj. secchkpntcount.

friend void checkpoint::enternotify(const roboobj &co);

Pozwala klasie checkpoint na wywołanie funkcji checkednotify.

robomap (roboobj *robo, word dx, word dy, screen *scr);

Konstruktor: parametr robo to robot, który będzie zabezpieczał checkpointy. Powinien on być jednocześnie ustawiony jako actobj. Inicjalizuje secchkpntcount i chkpntscount na 0.

bool allchecked() const { return secchkpntcount == chkpntscount; }

Zwraca true ó gdy wszystkie checkpointy zostały zabezpieczone.

bool generatecheckpoint(word tries);

Próbuje tries razy losować pozycję na mapie. Sprawdza, czy na niej jest pusty pixel. Jeżeli tak, tworzy nowego checkpointa z odpowiednim numerem, ustawia go tam i wychodzi. Zwraca true ó udało się wstawić checkpointa. Zwiększa chkpntscount o jeden.

roboobj

inline bool securecheckpoint(/* out */ checkpoint *&co);

Zabezpiecza checkpoint na aktualnej pozycji. Zwraca true, jeżeli został zabezpieczony. W parametrze co zwraca checkpoint na aktualnej pozycji lub 0, jeżeli nie ma.

Najpierw należy wywołać funkcję checkpos i przechować wynik. Jeżeli jest niezerowy to sprawdzamy, czy wskazuje na obiekt klasy checkpoint. Jeżeli tak, to należy wywołać funkcję checkpoint::enternotify, oraz do parametru przypisać otrzymany wskaźnik. W przeciwnym wypadku należy zwrócić false.

Jeżeli nie ma RTTI w kompilatorze (dynamic_cast), to należy zrobić wirtualną funkcję zwracającą id typu w klasie mapobj, i na jej podstawie wiedzieć, czy dany mapobj jest checkpointem.

roboobj(word x, word y, robomap &parent) : movmapobj(x, y, parent) {}

Jedyny konstruktor. Widzimy, że roboobj może być tylko na mapie typu robomap...

robomap &map () const;

… więc możemy spokojnie dokonać konwersji parent na robomap&....

checkpoint

word number;

Przechowuje numer checkpointa.

roboobj(word x, word y, robomap &parent, word number) : movmapobj(x, y, parent), number(number) {}

Jedyny konstruktor. Ustala odpowiednie zmienne. Checkpoint może być tylko na robomapie.

int enternotify(const roboobj &robo);

Informuje checkpoint o wejściu nań robota, ale powinien to sprawdzić. Zwraca -1 jak jeszcze nie został zabezpieczony, jak został to swój numer. W implementacji po sprawdzeniu pozycji oraz tego, czy wszystkie poprzednie checkpointy zostały zabezpieczone (number == robomap::secchkpntscount) wywołuje robomap::checkednotify.

robomap &map () const;

Konwersja parent na robomap.

robo

struct edge;

Struktura identyfikująca krawędź łączącą dwa checkpointy.

vector<byte> mem;

Mapa pamiętana przez robota, jej rozmiar poziomy i pionowy jest dwa razy większy niż rzeczywistej mapy, po zakończeniu przeszukiwania mapy i znalezieniu wszystkich checkpointów może zostać zwolniona.

vector<checkpoint *> chkpnts;

Przechowuje wskaźniki do już odkrytych i niezabezpieczonych checkpointów; indeks w tej tablicy jednoznacznie identyfikuje checkpointa.

word unsecchkpntscount;

Liczba niezabezpieczonych checkpointów po przeszukaniu mapy.

dynhalfarray2<path> paths;

Przechowuje ścieżki pomiędzy checkpointami.

vector<word> visited;

Wektor używany przy przeszukiwaniu w głąb.

tree t;

Zmienna pamiętająca minimalne drzewo rozpinające.

stack<word> s;

Stos używany przy przeszukiwaniu w głąb.

inline bool gotocheckpoint(word source, word dest);

Funkcja przechodzi od jednego checkpointa do drugiego po znalezionej ścieżce w tablicy paths. Aby nie trzymać dwóch kopii jednej ścieżki (od checkpointa x do y i odwrotnej), chodzimy po niektórych ścieżkach od tyłu.

Sprawdzamy, czy dest < source. Jeżeli tak to wywołujemy funkcję gotopath z parametrem paths[source][dest]. Jeżeli dest > source to wywołujemy funkcję gotorevpath z parametrem paths[dest][source]. Jeżeli dest == source to zwracamy true, inaczej zwracamy wartość zwróconą przez gotopath.

inline word delta(word source, word dest);

Zwraca odległość między checkpointami, wyciągniętą z tablicy paths (tj. rozmiar tej tablicy). Odpowiedni element ustalamy tak jak poprzednio.

bool gotopath(const path &co);

Przechodzi robotem po podanej ścieżce. Odczytuje kolejno ze ścieżki kierunki, w którym ma się poruszyć i czyni to. Nie sprawdza, czy weszło na jakiś obiekt. Jeżeli nie udało się wejść na jakiś pixel z powodu ściany, funkcja zwraca false.

bool gotorevpath(const path &co);

To samo co poprzednia funkcja, tylko przechodzi ściezkę od tyłu.

void play ();

Główna pętla działań robota. Ma na celu zabezpieczenie wszystkich checkpointów.

robo(word x, word y, robomap &parent) : roboobj(x, y, parent) {}

Konstruktor. Przekazuje parametry do konstruktora klasy bazowej.

map::plotter

map *m;

Przechowuje wskaźnik na mapę, która będzie rysowana.

dword baseoffset;

Offset bazowy. Jest to offset w tablicy tego pixela, który będzie narysowany jako pierwszy w podanej w wywołaniu screen::put pozycji.

plotter(map *m, dword baseoffset) : m(m), baseoffset(baseoffset) {}

Konstruktor ustawiający parametry.

inline screen::attr operator()(word offset) const { return m->getattr(baseoffset + offset); }

Operator pozwalający używać obiektu jak funkcji. Zwraca atrybuty tego pixela, który jest w tym samym wierszu, co pixel bazowy i w kolumnie o offset oddalonej na prawo od bazowej.

Implementacja wywołuje po prostu map::attr z parametrem równym sumie offset i baseoffset.

screen

word fdx;

word fdy;

Rozmiar ekranu w pixelach

struct attr {

char ch; // znak

byte cl; // kolor

attr(ch, cl): ch(ch), cl(cl) {}

};

Struktura przechowująca atrybuty pixela.

word dx() const { return fdx; }

word dy() const { return fdy; }

Zwracają rozmiary ekranu.

virtual bool open();

Inicjalizuje ekran do użycia.

virtual void close();

Zamyka ekran.

virtual void put (word y, word x, attr pixel) =0;

Wypełnia podany pixel podanymi atrybutami.

virtual void put(word y, word x, word dx, map::plotter &) =0;

Wypełnia dx pixeli w wierszy y zaczynając od pixela w kolumnie x atrybutami podawanymi przez obiekt klasy map::plotter. Atrybuty i+x pixela w wierszu y otrzymujemy wywołując map::plotter::operator() z parametrem i.

queue

word beg;

Index tego elementu tablicy, który jest pierwszy do zdjęcia

word end; I

Index tego elementu tablicy, w którym się powinno dostawić nowy element

queue();

Konstruuje kolejkę o rozmiarze 0.

queue(word size);

Konstruuje kolejkę o rozmiarze size.

ins(const T &co);

Wstawia nowy element na kolejkę.

T pop();

Zdejmuje element z kolejki i go zwraca.

T *begin()

Zwraca początek tablicy elementów na kolejce, czyli początek tablicy przesunięty o beg.

 

5. Uwagi dodatkowe

Należy zakodować jedną z klas dosscreen, winconscreen lub linuxscreen, używając funkcji specyficznych dla danego systemu operacyjnego. W przypadku dosscreen należy zapisywać dane bezpośrednio do pamięci.

Wyjaśnienia wymaga także konstrukcja funkcji screen::put(map::plotter &). Chodzi o to, aby nie trzeba było wywoływać funkcji wirtualnej dla każdego pixela oraz żeby nie trzeba było buforować całych linii w pamięci przed przesłaniem ich na ekran. Niestety, aktualnie kompilatory nie wspierają wirtualnych funkcji template'owych, więc nie da się tego zrobić bardziej uniwersalnie. Chociaż to tez nie jest najlepiej, ale zapewnia maksimum szybkości (przy inlinowaniu).

Klasa map powinna wspierać wyświetlanie tylko pewnego okna na mapę o wielkości ekranu komputera. Zmienne map::vx i map::vy oznaczają współrzędne na mapie pierwszego widocznego pixela na ekranie. Po każdym ruchu robota ekran powinien być aktualizowany. Jeżeli potrzebne jest przesunięcie okna (jeżeli robot przejdzie za blisko krawędzi ekranu), należy narysować całą mapę od początku, w przeciwnym wypadku wystarczy odświeżyć tylko zmienione pixele. Na ekranie powinna być odzwierciedlona różnica między odwiedzonymi i nieodwiedzonymi pixelami. Także zabezpieczony checkpoint powinien wyświetlać swój numer. Powinna być widoczna różnica pomiędzy zabezpieczonym i niezabezpieczonym checkpointem.

Typ screen::attr ukrywa atrybuty pojedynczego pixela ekranu. Są to: znak w kodzie ASCII i kolor znaku oraz tła - znaczenie specyficzne dla implementacji - jeżeli zaistnieje potrzeba, można zmienić typ screen::attr tak, aby lepiej odzwierciedlał możliwości prezentacji na ekranie, np. w trybie graficznym.

Do klasy screen można dodać funkcje obsługujące funckje specyficzne dla implementacji, np. wypisanie ciągu znaków na określonej pozycji, wczytanie ciągu znaków.

W przypadku implementacji w trybie tekstowym należy użyć trybu 80x50 znaków.

Poniżej znajduje się kilka rysunków pokazujących różne strategie chodzenia robota. Pierwsza z nich jest zbliżona do algorytmu rzeczywiście zastosowanego, w pewnym momencie pominięto ściany ograniczające mapę.

Druga strategia przechodzi zawsze ściany równoległe do krawędzi pierścieni przed szukaniem najbliższego nieodwiedzonego pixela. Ta wersja nie została zaimplementowana.

Ten dokument znajduje się pod adresem http://mar.prv.pl/education/piwut.htm

oraz http://mar.prv.pl/education/piwut.doc.